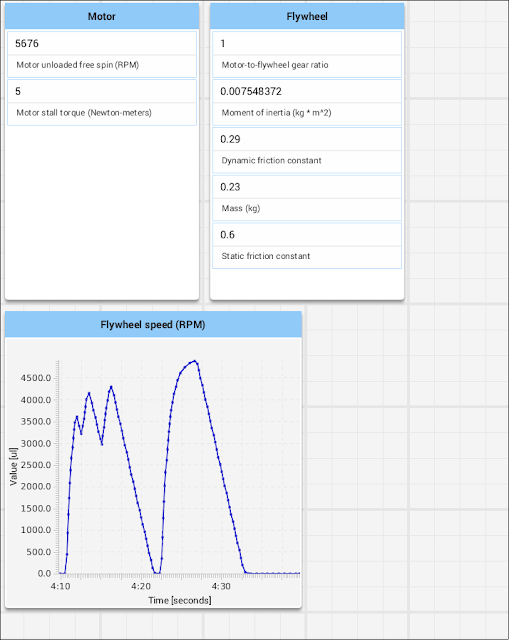
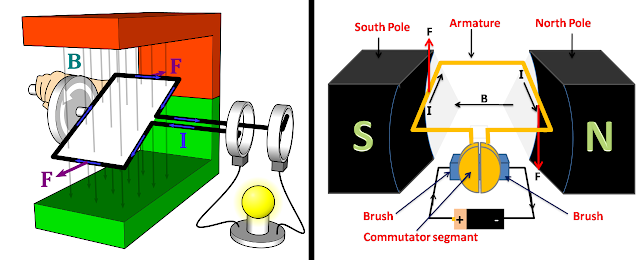
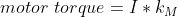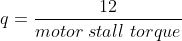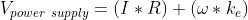On a previous post, I discussed creating a simulator for a simple flywheel in the FIRST Robotics WPILib framework in Java. We last discussed the high-level framework and simulating a motor; here, we’ll go into simulating friction and how we put it all together.
Friction is deceptively complicated
On the surface, friction is extremely simple. As is taught in high school
physics, it’s the force that resists motion proportional to the normal force of
the surface pushing against gravity. Which is to say, it’s just
-K<sub>d</sub> * m * g, for g the gravitational constant (acceleration) and
m the mass of the object, and K<sub>d</sub> the dynamic friction
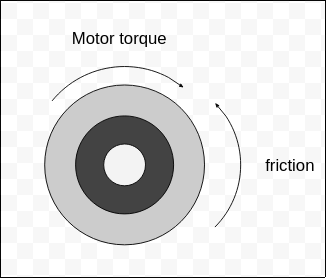
coefficient. Since the flywheel’s axle is pushed down by gravity on its socket,
the friction force becomes a counter-torque opposing spin. So, no problem. We
calculate the counter-torque, subtract it from the motor’s forward torque, and
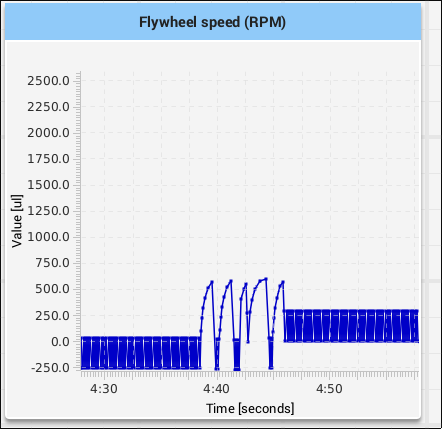
update every step. Punch that in and… Oh dear.
The problem is that friction is a continuous effect: the force opposing motion applies until the object gets very close to zero velocity (relative to the surface it’s rubbing against). At that point, the molecules of the two objects “gum up” with each other and the object stops moving. But the simulator is a discrete time-step simulation: every time step, the forces acting on the flywheel are summed up, velocity is changed, and then it’s assumed the flywheel velocity stays the same until the next time step. So the velocity “wiggles” back and forth around zero without ever reaching zero and the flywheel never actually stops.
There are several solutions of various levels of complexity for handling this aspect of friction, but for our purposes we can use a fairly simple one:
- Calculate the new angular velocity from the torques and counter-torques.
- Check to see if the sign of the velocity has flipped. If it has, we know the velocity crossed through the zero boundary.
- If we did cross zero, check to see if the driven torque exceeds the counter torque.
- If it doesn’t, the motor seizes; set velocity to zero.
Code as follows:
if (Math.signum(newAngularVelocityRps) != Math.signum(flywheelAngularVelocityRps)
&& flywheelAngularVelocityRps != 0
&& newAngularVelocityRps != 0) {
// Crossed zero boundary; if torque is too low to overcome friction, motor seizes
if (Math.abs(advantagedTorque) < Math.abs(counterTorque)) {
newAngularVelocityRps = 0;
}
}
One other aspect of friction to account for: Static friction generally exceeds dynamic friction, and applies if the flywheel is starting from zero velocity. We account for that by selecting the right friction coefficient based on whether the motor is moving and comparing the torque to the counter-torque from the friction; if driven torque does not exceed counter-torque, the motor doesn’t start.
var frictionCoefficient = m_motorSpeedRpm == 0 ?
m_flywheelStaticFrictionConstant.getDouble(1.0) :
m_flywheelDynamicFrictionConstant.getDouble(1.0);
// ...
var totalTorque = advantagedTorque - counterTorque;
if (m_motorSpeedRpm == 0 && Math.abs(advantagedTorque) < Math.abs(counterTorque)) {
// stalled motor does not overcome static friction
totalTorque = 0;
}
Putting it all together
Having accounted for friction, we now only need to take the total torques computed and apply them to how the velocity and encoder count changes over time.
To start, the total torque changes the angular velocity. Similar to the famous F = ma equation,
torque = moment of inertia * angular acceleration. So we divide our torque by the moment of inertia
to get an acceleration, and add it (times the time delta step) to the velocity:
var angularAccelerationRadsPerSec = totalTorque / m_flywheelMomentOfInertiaKgMSquared.getDouble(1.0);
var flywheelAngularVelocityRps = Units.rotationsPerMinuteToRadiansPerSecond(m_motorSpeedRpm) / gearRatio;
// Update angular velocity, parceling the change by the delta-T
var newAngularVelocityRps = flywheelAngularVelocityRps + angularAccelerationRadsPerSec * TIMESTEP_SECS;
Then, we just need to update the velocity and position for the encoder, and update the RPM graph:
m_motorSpeedRpm = Units.radiansPerSecondToRotationsPerMinute(newAngularVelocityRps * gearRatio);
// multiply by timestep and ratio of rotations to radians to get new flywheel position
var flywheelSpeedRotationsPerSec = newAngularVelocityRps / (2 * Math.PI);
var flywheelDelta = flywheelSpeedRotationsPerSec * TIMESTEP_SECS;
// encoder values are relative to flywheel, not motor
m_encoder.setDistance(m_encoder.getDistance() + flywheelDelta);
m_encoder.setRate(newAngularVelocityRps);
m_flywheelSpeedRpm.setDouble(flywheelSpeedRotationsPerSec * 60);
And we’re done! We have a self-updating flywheel simulation that we can experiment with.